在上一篇文章中,我们次要介绍了一些根底的常用面积公式,并简单申明了外接圆和内切圆,本文会介绍别的一种与三角形相关的圆——旁切圆,它是由两个角的外角平分线和别的一个角的平分线交于一点而得到的,并连系内切圆,得出与之相关的面积公式,同时会导出一些三角形的边角关系,尤其是三角形中的半角公式。
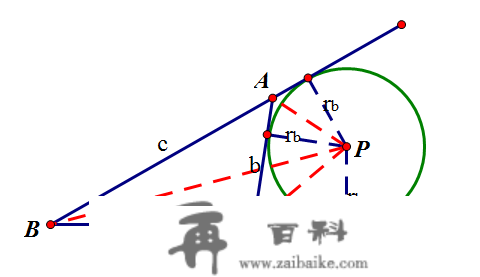
如上面的三角形旁切圆图所示,圆P为三角形ABC边AC上的旁切圆,其半径为rbr_b,三边为a,b,c。在那里,我们约定,rar_a,rbr_b,rcr_c别离暗示,以BC、AC、AB边上的旁切圆的半径。操纵公式五的推导法子,同样将三角形ABC面积朋分求解,由图能够看出:
S△=S△PBA+S△PBC−S△PACS_\triangle =S_{\triangle PBA}+S_{\triangle PBC}-S_{\triangle PAC}=12⋅c⋅rb+12⋅a⋅rb−12⋅b⋅rb=\frac{1}{2}\cdot c\cdot r_b+\frac{1}{2}\cdot a\cdot r_b-\frac{1}{2}\cdot b\cdot r_b=12(c+a−b)rb=\frac{1}{2}(c+a-b)r_b=(p−b)rb=(p-b)r_b
同理,对别的两个旁切圆也有类似的式子,即:
S△=(p−a)ra=(p−b)rb=(p−c)rcS_{\triangle}=(p-a)r_{a}=(p-b)r_{b}=(p-c)r_{c}
记为公式十一。
公式十一的思绪和内切圆朋分求面积的思绪是一样的,只是旁切圆在三角形外面,就有了减法,也就是有了负号,那个特点在以后的内容中仍然会表现,除去负号,发现旁切圆和内切圆的许多性量都是类似的。
操纵海伦公式S△=p(p−a)(p−b)(p−c)S_\triangle =\sqrt{p(p-a)(p-b)(p-c)} (公式八)和S△=rpS_\triangle =rp,消去(p-a),(p-b),(p-c),p得到:
S△=rrarbrcS_{\triangle}=\sqrt{rr_{a}r_{b}r_{c}}
记为公式十二。
公式十二从形式上间接将三角形的根本元素a、b、c三边与A、B、C三角都消弭了,可见,我们之前所说的,因为每一个三角形都有独一一个确定的内切圆和三个独一确定的旁切圆,于是那些圆就是三角形的根本属性,因而那些圆的半径rr,rar_a,rbr_b,rcr_c与边长和角度一样,都是三角形的根本元素,它们之间能够互相导出。
由公式五和公式十一,变形能够得到:1r=pS△\frac{1}{r} = \frac{p}{S_\triangle} ,1ra=p−aS△\frac{1}{r_a} = \frac{p-a}{S_\triangle} ,1rb=p−bS△\frac{1}{r_b} = \frac{p-b}{S_\triangle} ,1rc=p−cS△\frac{1}{r_c} = \frac{p-c}{S_\triangle},于是有:
1ra+1rb+1rc\frac{1}{r_a} + \frac{1}{r_b} + \frac{1}{r_c }=p−aS△+p−bS△+p−cS△= \frac{p-a}{S_\triangle} + \frac{p-b}{S_\triangle} + \frac{p-c}{S_\triangle}=3p−a−b−cS△=pS△=1r= \frac{3p-a-b-c}{S_\triangle } = \frac{p}{S_\triangle} = \frac{1}{r}
于是我们得到了一个关于三角形内切圆半径和三个旁切圆半径的一个关系式,即:
1r=1ra+1rb+1rc\frac{1}{r} = \frac{1}{r_a} + \frac{1}{r_b} + \frac{1}{r_c }
由公式五和公式十二,将内切圆半径消掉,则有:
S△=rarbrcpS_{\triangle}=\frac{r_{a}r_{b}r_{c}}{p}记为公式十三。
由公式十一变形能够得到:ra=S△p−ar_{a} = \frac{S_\triangle}{p-a} ,rb=S△p−br_{b} =\frac{S_\triangle}{p-b} ,rc=S△p−cr_{c} =\frac{S_\triangle}{p-c} ,由公式五变形得到:r=S△pr =\frac{S_\triangle}{p} ,于是有:
ra+rb+rc−rr_a+r_b+r_c-r
=S△p−a+S△p−b+S△p−c−S△p=\frac{S_\triangle}{p-a} +\frac{S_\triangle}{p-b} +\frac{S_\triangle}{p-c} -\frac{S_\triangle}{p}
=S△⋅p(p−a)(p−b)(p−c)⋅abcp(p−a)(p−b)(p−c)= \frac{S_{\triangle } \cdot p(p-a)(p-b)(p-c)\cdot abc}{p(p-a)(p-b)(p-c)}
=S△⋅abc=4R=S_{\triangle } \cdot abc=4R
(由公式三得到)
于是我们得到了一个关于三角形的外接圆半径,内切圆半径,旁切圆半径之间的关系式,即:
ra+rb+rc−r=4Rr_a+r_b+r_c-r=4R
我们能够从中看出,外接圆、内切圆、旁切圆是可以间接成立联络的,隐藏了它们中间的三角形前言,那给我们的启发是,当我们发现两个看似不相关的事物时,例如独立的两个圆,但是现实上它们是彼此联络的,只是联络的前言我们没瞧见,那里就是三角形,又或者能够说成是当两个事物已经有了相关的联络时,独立研究它们也许找不出此中的原理,那么我们就能够试着去想想它们之间能否存在一个中间的前言。
接着我们再回头切磋一下内切圆的性量。
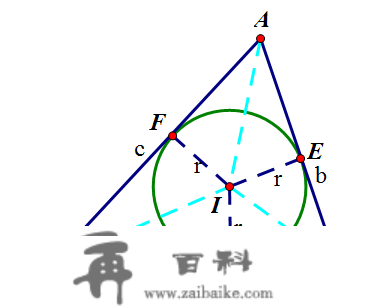
如上面的内切圆图所示,因为内切圆圆心是三条角平分线的交点,于是由角平分线的性量能够得到,AE=AF,BF=BD,CE=CD,从而有:
p=12(a+b+c)p=\frac{1}{2}(a+b+c)
=12(AE+EC+CD+BD+BF+FA)=\frac{1}{2}(AE+EC+CD+BD+BF+FA)
=12(2AE+2EC+2BD)=\frac{1}{2}(2AE+2EC+2BD)
=b+BD=b+BD
即 BD=BF=p−bBD =BF=p-b ,同理,有a,c两边的式子成立。
于是:
tanB2=rp−b=S△p(p−b)=(p−a)(p−c)p(p−b)tan\frac{B}{2} = \frac{r}{p-b} = \frac{S_\triangle }{p(p-b)} =\sqrt{\frac{(p-a)(p-c)}{p(p-b)}}
同理:
何中华 tanA2=rp−a=S△p(p−a)=(p−b)(p−c)p(p−a)tan\frac{A}{2} = \frac{r}{p-a} = \frac{S_\triangle}{p(p-a)} =\sqrt{ \frac{(p-b)(p-c)}{p(p-a)} }
tanC2=rp−c=S△p(p−c)=(p−a)(p−b)p(p−c)tan\frac{C}{2} = \frac{r}{p-c} = \frac{S_\triangle }{p(p-c)} = \sqrt{ \frac{(p-a)(p-b)}{p(p-c)}}
那组公式被称为三角形的半角公式。
由半角公式能够变形三角形的一组面积公式:
S△=p(p−a)tanA2=p(p−b)tanB2=p(p−c)tanC2S_{\triangle}=p(p-a)tan\frac{A}{2}=p(p-b)tan\frac{B}{2}=p(p-c)tan\frac{C}{2}
记为公式十四。
由公式十四能够得到:
tanA2tanB2tanC2tan\frac{A}{2} tan\frac{B}{2} tan\frac{C}{2}=S△p(p−a)⋅S△p(p−b)⋅S△p(p−c)= \frac{S_\triangle}{p(p-a)} \cdot \frac{S_\triangle}{p(p-b)} \cdot \frac{S_\triangle}{p(p-c)}
=S△2p(p−a)(p−b)(p−c)⋅S△p2=S△p2= \frac{S_\triangle^{2}}{p(p-a)(p-b)(p-c)} \cdot \frac{S_\triangle}{p^2} = \frac{S_\triangle}{p^2}
(操纵海伦公式消弭)
即:
S△=p2tanA2tanB2tanC2S_{\triangle}=p^{2}tan\frac{A}{2}tan\frac{B}{2}tan\frac{C}{2}
记为公式十五。
操纵三角函数之间的关系,能够推出三角形的正弦和余弦的半角公式,那里我们不证明,间接给出成果。
sinA2=(p−b)(p−c)bcsin \frac{A}{2} = \sqrt{\frac{(p-b)(p-c)}{bc}}
sinB2=(p−a)(p−c)acsin\frac{B}{2} = \sqrt{ \frac{(p-a)(p-c)}{ac}}
sinC2=(p−a)(p−b)absin \frac{C}{2} = \sqrt{\frac{(p-a)(p-b)}{ab}}
cosA2=p(p−a)bccos\frac{A}{2} =\sqrt{\frac{p(p-a)}{bc}}
cosB2=p(p−b)accos\frac{B}{2} = \sqrt{\frac{p(p-b)}{ac}}
cosC2=p(p−c)abcos\frac{C}{2} = \sqrt{\frac{p(p-c)}{ab}}
与公式十五的推导一样,我们能够正弦和余弦的半角公式别离得出别的两个三角形面积公式:
S△=abcpcosA2cosB2cosC2S_{\triangle}=\frac{abc}{p}cos\frac{A}{2}cos\frac{B}{2}cos\frac{C}{2}
S△=abcpsinA2sinB2sinC2S_{\triangle}=abcpsin\frac{A}{2}sin\frac{B}{2}sin\frac{C}{2}
别离记为公式十六、公式十七。
将公式四S△=abc4RS_\triangle = \frac{abc}{4R}带入公式公式十七,消去abc,得:
S△=4RpsinA2sinB2sinC2S_{\triangle}=4Rpsin\frac{A}{2}sin\frac{B}{2}sin\frac{C}{2}
记为公式十八。
由公式十五、公式十六、公式十八并比照公式五S△=rpS_\triangle =rp,能够得到r=ptanA2tanB2tanC2=4RsinA2sinB2sinC2r=p tan\frac{A}{2} tan\frac{B}{2} tan\frac{C}{2}=4R sin\frac{A}{2}sin\frac{B}{2} sin\frac{C}{2},p=4RcosA2cosB2cosC2p=4R cos\frac{A}{2} cos\frac{B}{2} cos\frac{C}{2},于是能够将公式十六中的abc和p消弭掉,得到:
S△=4RrcosA2cosB2cosC2S_{\triangle}=4Rrcos\frac{A}{2}cos\frac{B}{2}cos\frac{C}{2}
记为公式十九。
同时也得到了一个边长与表里接圆半径的式子:4Rr=abcp4Rr= \frac{abc}{p} 。
将r=ptanA2tanB2tanC2r=p tan\frac{A}{2} tan\frac{B}{2} tan\frac{C}{2}代入公式十五中消去p,便有:
S△=r2tanA2tanB2tanC2=r2cotA2cotB2cotC2S_{\triangle}=\frac{r^{2}}{tan\frac{A}{2}tan\frac{B}{2}tan\frac{C}{2}}=r^{2}cot\frac{A}{2}cot\frac{B}{2}cot\frac{C}{2}
记为公式二十。
与公式六S△=r2(cotA2+cotB2+cotC2)S_\triangle =r^2 (cot\frac{A}{2}+cot\frac{B}{2}+cot\frac{C}{2})停止比照,我么能够发现一个等式:
cotA2cotB2cotC2=cotA2+cotB2+cotC2cot\frac{A}{2}cot\frac{B}{2}cot\frac{C}{2}= cot\frac{A}{2}+cot\frac{B}{2}+cot\frac{C}{2}
。
总结:本文所推导出的十个面积公式均与三角形的内切圆和旁切圆有关,同时还导出了半角公式,在处置有关内切圆和旁切圆与面积相关的问题上将会出格有用。除此之外,公式二十与前文中的公式四和公式六的形式以及它们所代表的几何意义值得深切探究,那将会在《周长为面积之变革率》一文中详细讲述,那里不再赘述。
